ترم جمع (OR)

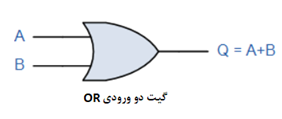
درحالی‌که، تابع AND، معمولا به‌عنوان عبارت حاصل‌ضرب است؛ تابع OR به‌عنوان ترم جمع شناخته می‌شود. تابع OR، معادل ریاضیاتی جمع است؛ که با نماد به‌علاوه (+) بیان می‌شود. از این‌رو، گیت OR با دو ورودی، دارای ترم خروجی است؛ که بیان بولی آن، A+B است؛ زیرا مجموع منطقی A و B می‌باشد.

گیت OR (جمع)

این جمع منطقی، معمولا به‌عنوان جمع بولی شناخته می‌شود؛ زیرا یک تابع OR، جمع ترم دو یا چند متغیر یا ثابت ورودی است. بنابراین، معادله‌ی بولی برای گیت OR با دو ورودی به‌صورت: Q=A+B است و Q برابر با A OR B می‌باشد. برای یک ترم جمع، این متغیرهای ورودی، می‌تواند “صحیح (true)” یا “غلط (false)”، “1” یا “0” یا مکمل آن‌ها باشند.

بنابراین؛ در جبر بولی، “جمع” به‌معنای OR نمودن عبارت‌ها با متغیرهای عبارت جمع است؛ که یک مثال شکل واقعی یا مکمل دارد؛ به‌طوری‌که جمع را نمی‌توان بیشتر ساده کرد. این ترم‌ها به‌عنوان ترم حداکثر (maxterms) نیز شناخته می‌شوند. این ترم ماکزیمم، مجموع مکمل تمام متغیرها یا ثابت‌ها با و یا بدون وارون‌سازی در عبارت بولی است. حال چگونه می‌توانیم عملکرد این تابع “جمع” را در جبر بولی، نشان دهیم؟!

یک عبارت جمع می‌تواند یک یا دو متغیر مستقل مانند A و B یا یک یا دو ثابت 0 و 1 داشته باشد. می‌توانیم از این متغیرها و ثابت‌ها در انواع ترکیب‌های مختلف استفاده کنیم و نتیجه‌ی جمع را همانطور که در لیست‌های زیر آمده است؛ نشان دهیم.

ترم‌های جمع جبر بولی

توجه داشته باشید؛ که “متغیر” بولی، می‌تواند یکی از دو مقدار “1” یا “0” را داشته باشد و مقدار خود را تغییر دهد. برای مثال، A=0 یا A=1. درحالی‌که، یک “ثابت” بولی می‌تواند یکی از دو شکل “1” یا “0” را داشته باشد که مقدار ثابت است و بنابراین، نمی‌تواند تغییر کند.

پس می‌توانیم ببینیم؛ که هر جمع بولی داده‌شده را می‌توان به یک ثابت یا متغیر تنها، ساده‌سازی کرد. توضیح مختصری از قوانین بولی مختلف در ادامه آمده است؛ که در آن “A” یک ورودی متغیر را نشان می‌دهد.

قانون خنثی‌کردن (Annulment Law):  یک عبارت OR شده با 0 ، همیشه برابر با خودش است(A+0=A)

قانون تطابق (Identity Law): یک عبارت OR شده با 1 ، همیشه برابر با 1 است(A+1=1)

قانون همانی (Idempotent Law):  یک عبارت OR شده با خودش ، همیشه برابر با خود عبارت است(A+A=A)

قانون متمم (Complement Law):  یک عبارت OR شده با مکمل خود ، همیشه برابر با 1 است(A+Ā=1)

قانون جابجایی (Commutative Law): ترتیب در دو عبارت که باهم OR شده‌اند، یکسان است.(A+1=1+A)

ترم ضرب (AND)

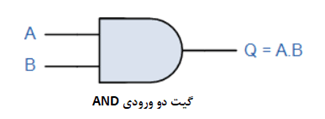
درحالی‌که، تابع OR معمولا، به‌عنوان ترم جمع شناخته می‌شود؛ تابع AND، به‌عنوان عبارت حاصل‌ضرب است. تابع AND، معادل ریاضیاتی ضرب است؛ که با علامت ضربدر (x) یا ستاره (*) نشان داده می‌شود. بنابراین،  گیت AND با دو ورودی، دارای ترم خروجی است؛ که بیان بولی آن، A.B است؛ زیرا حاصل‌ضرب منطقی A و B می‌باشد.

گیت AND (ضرب)

این ضرب منطقی، معمولا به‌عنوان ضرب بولی شناخته می‌شود؛ زیرا یک تابع AND، ضرب دو یا چند ترم متغیر یا ثابت ورودی است. اما اکنون، باید بخاطر بسپاریم؛ که تابع AND، نشان‌دهنده‌ی عبارت حاصل‌ضرب است.

حاصل‌ضرب جمع

تا اینجا مشاهده کردیم؛ که تابع OR، مجموع منطقی جمع بولی و تابع AND ، حاصل‌ضرب منطقی ضرب بولی را تولید می‌کند. اما هنگام سروکار داشتن با مدارهای منطقی ترکیبی که در آنها، گیت‌های AND، گیت‌های OR و گیت‌های NOT به‌هم متصل شده‌اند؛ عبارت‌ حاصل‌ضرب جمع‌ها، به‌صورت گسترده‌ای کاربرد دارد.

حاصل‌ضرب جمع (POS) از این واقعیت ناشی می‌شود؛ که دو یا چند مجموع (ORشدن)، در هم ضرب (ANDشدن) شده‌اند. به این معنا، که خروجی‌های دو یا چند گیت OR به ورودی گیت AND متصل می‌شوند تا به‌طور موثری باهم AND شوند و خروجی منطقی OR-AND نهایی را ایجاد نمایند. برای مثال، تابع بولی زیر، یک عبارت حاصل‌ضرب جمع معمولی است:

عبارت‌های حاصل‌ضرب جمع

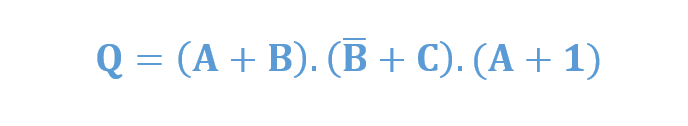
و نیز،

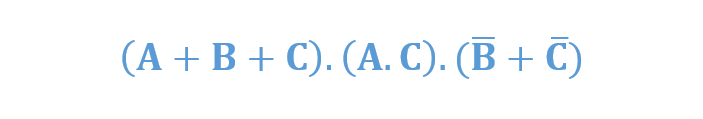
با این‌حال، توابع بولی می‌توانند به‌صورت اشکال غیراستاندارد حاصل‌ضرب جمع‌ها، همانند آنچه در زیر آمده است؛ نشان داده شوند؛ اما می‌توان با استفاده از قانون توزیع‌پذیری، عبارت را گسترش داده و آن را به فرم POS استاندارد، تبدیل کرد. بنابراین:

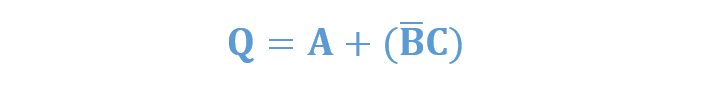
ترم‌های گسترش‌یافته‌ی حاصل‌ضرب جمع به‌صورت زیر در می‌آیند:

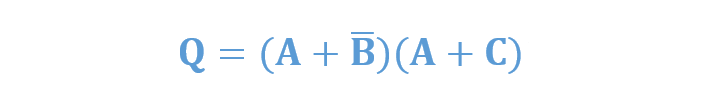
یک مثال غیراستاندارد دیگر به‌صورت زیر است:

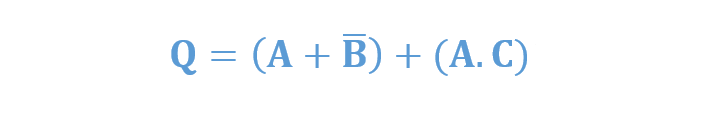
ترم‌های گسترش‌یافته‌ی حاصل‌ضرب جمع به‌صورت زیر در می‌آیند:

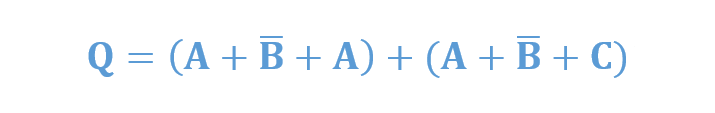
که در صورت لزوم می‌توان با استفاده از قانون توزیع‌پذیری و قانون جذب، آن را کاهش داد:

تبدیل یک عبارت POS به یک جدول درستی

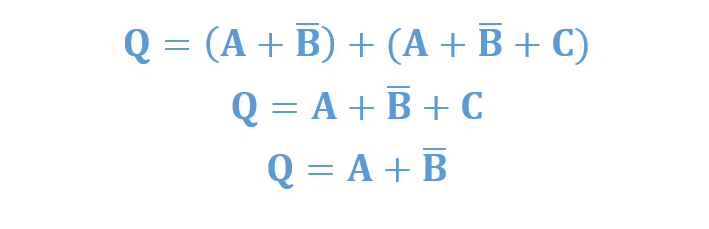
ما می‌توانیم هر عبارت حاصل‌ضرب-جمع را به شکل جدول درستی نمایش دهیم؛ از آنجایی‌که هر ترکیب ورودی که خروجی منطقی “0” را تولید کند. یک ترم جمع یا OR است؛ همانطور که در شکل زیر آمده است.

عبارت حاصل‌ضرب جمع زیرا را در نظر بگیرید:

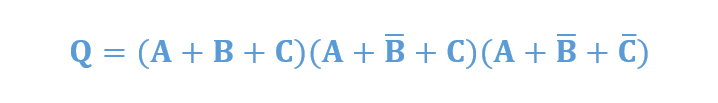
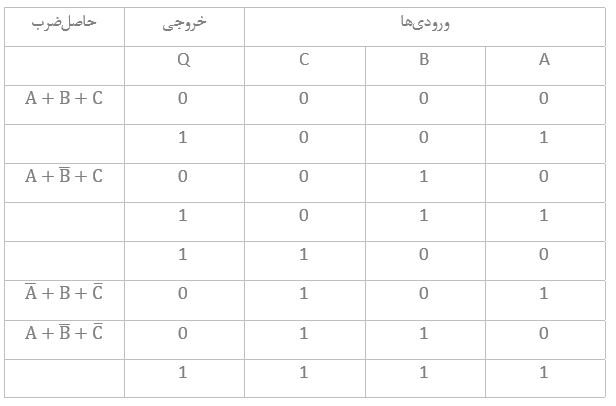
اکنون می‌توانیم، جدول درستی را برای عبارت بالا، ترسیم کنیم، تا فهرستی از تمام ترکیب‌های ورودی ممکن برای A، B و C نشان داده شود؛ که منجر به خروجی “0” می‌شود.

جدول درستی حاصل‌ضرب جمع

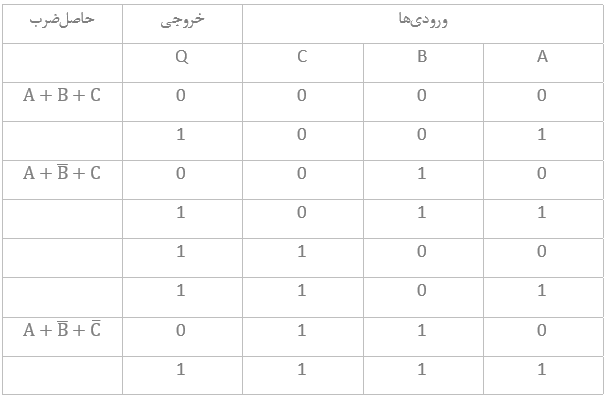
پس می‌توانیم به‌وضوح از جدول درستی ببینیم؛ که هر ردیفی که برای خروجی‌اش “۰” تولید می‌کند؛ با عبارت جمع بولی آن مطابقت دارد و همه‌ی سطرهای دیگر، خروجی “۱” دارند. مزیت در اینجا، این است؛ که جدول درستی، یک نشانه‌ی بصری از عبارت بولی به ما می‌دهد و به ما امکان می‌دهد؛ عبارت را ساده کنیم و بخاطر بسپاریم که یک عبارت جمع، خروجی “۰” را زمانی تولید می‌کند که همه‌ی ورودی‌های آن، “۰” باشند. بنابراین برای ایجاد یک ردیف ترم مجموع برابر با “۰”، باید تمام ورودی‌هایی که برابر با “۱” می‌باشند را معکوس کنیم.

مثال حاصل‌ضرب- جمع

عبارت جبر بولی زیر، به این صورت داده شده‌است:

1. با استفاده از جدول درستی، تمام ترکیب‌بندی‌های ممکن را برای شرایط ورودی، که سبب تولید خروجی “۰” می‌شوند؛ نشان دهید.
2. یک دیاگرام گیت منطقی برای عبارت POS، رسم کنید.

• جدول درستی:

• دیاگرام گیت منطقی

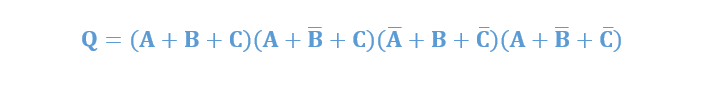
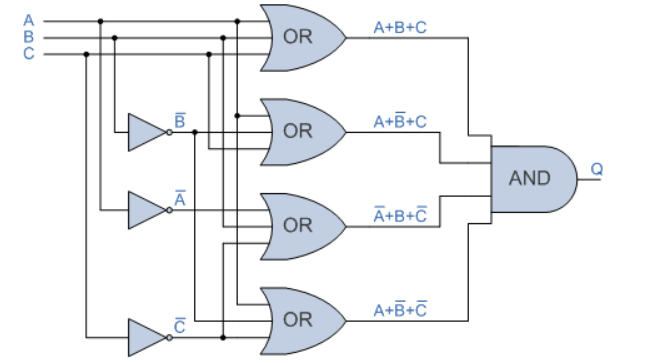
بنابراین؛ عبارت حاصل‌ضرب‌-جمع (POS)، یک عبارت بولی استاندارد است؛ که دو یا چند “جمع” را در هم “ضرب می‌کند” و برای یک مدار منطقی دیجیتال، عبارت POS به این صورت است؛ که خروجی، شامل دو یا چند گیت منطقی OR است، که باهم AND شده‌اند؛ تا خروجی منطقی نهایی (OR-AND) را بسازند.