نمایش کسری اعداد باینری از قوانین مشابه حاکم بر اعداد دسیمال پیروی می‌­کند، با این تفاوت که هر رقم باینری از سیستم شماره گذاری بر مبنای ۲ استفاده خواهد کرد.

دستگاه اعداد اعشاری یا دسیمال (Decimal) از سیستم شماره گذاری بر مبنای ده (Base-of-10) استفاده می­‌کند، که در آن هر یک از ارقام تشکیل دهنده عدد نهایی، می­تواند یکی از ده مقدار ممکن در محدوده 0 تا 9 را اختیار کند. بنابراین با حرکت از سمت راست به چپ در امتداد یک عدد دسیمال، هر رقم دارای ارزش ده برابر بیشتر از رقم به سمت راست خود خواهد بود. به صورت مشابه با حرکت از سمت چپ به راست در امتداد ارقام یک عدد دسیمال، هر رقم ارزشی معادل ده برابر کوچکتر از عدد سمت چپ خود را اختیار ­می­‌کند.

با ادامه حرکت به سمت راست و رسیدن به عدد صفر (نقطه شروع اعداد اعشاری decimal point (ممیز)) اعداد کسری باینری معرفی خواهند شد.

اعداد کسری معمولی (A Typical Fractional Number)

برای مثال در عدد دسیمال ۱۲۳۴.۵۶۷ اولین عدد پس از نقطه دسیمال (عدد ۵) دارای ارزش یک دهم (۰.۱) برابری رقم سمت چپ خود (عدد ۴ دارای ارزش ۱) است. بنابراین با حرکت به سمت راست ارزش هر رقم یک دهم مقدار ارزش رقم سمت چپ خود خواهد بود.

در سیستم شماره گذاری دسیمال با استفاده از یک نماد موقعیتی (نقطه دسیمال) ارزش هر رقم نسبت به موقعیت آن مشخص خواهد شد، به بیان دیگر هر رقم با توجه به موقعیت آن رقم در دو طرف نقطه دسیمال مقدار وزن متفاوتی را اختیار می‌­کند.

در سیستم شماره گذاری استاندارد ده­دهی جهت نمایش ارقام سمت چپ نقطه دسیمال، مقادیر به صورت زیر معرفی خواهند شد.

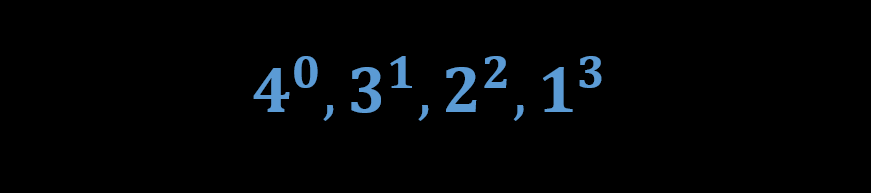
به همین ترتیب، جهت نمایش اعداد کسری در سمت راست نقطه دسیمال، از فرمت زیر پیروی می‌­شود.

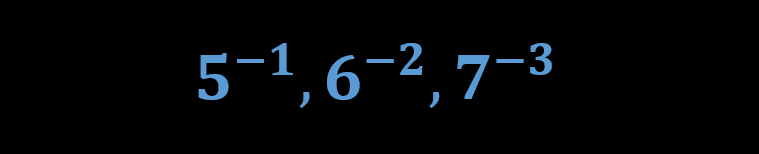
بنابراین معرفی یک عدد دسیمال، براساس فرمت فوق، رابطه میان وزن هر رقم و موقعیت آن رقم را نشان می­دهد. مقدار هر عدد دسیمال از محاسبه مجموع ارقام آن عدد ضرب در وزن مربوطه حاصل خواهد شد. بنابراین عدد دسیمال ۱۲۳۴.۵۶۷ به صورت زیر معرفی می‌شود.

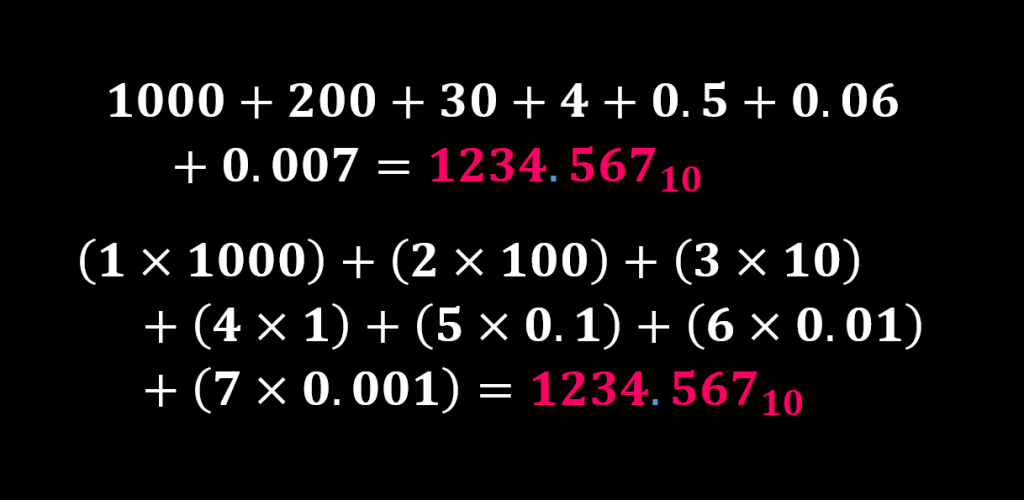
و یا به صورت چند جمله‌ای زیر:

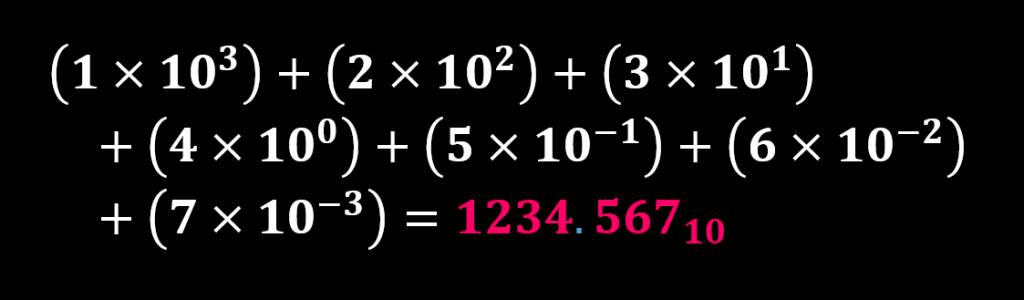
استفاده از مفهوم نماد موقعیتی در سیستم شماره گذاری باینری مفهوم مشابه با اعداد دسیمال خواهد داشت. به این صورت که هر رقم با توجه به موقعیتی که در این سیستم اختیار می­کند، دارای ارزش و وزن متفاوتی خواهد بود، با این تفاوت که وزن هر رقم نسبت به ارقام مجاور با ضریب ۲ تغییر خواهد کرد.

کسرهای باینری (Binary Fractions)

سیستم شماره گذاری باینری یک سیستم شماره گذاری بر مبنای ۲ است، که هر رقم می­‌تواند تنها یکی از دو مقدار ممکن ۰ یا ۱ را اختیار کند.

مشابه با اعداد کسری دسیمال، اعداد کسری بدون علامت باینری را می­توان با قرار دادن ارقام باینری در سمت راست نقطه باینری (مشابه با نقطه دسیمال در سیستم شماره گذاری دسیمال) معرفی کرد. بنابراین با معرفی ارقام در سمت راست نقطه باینری کسرهای باینری ایجاد می­‌شوند.

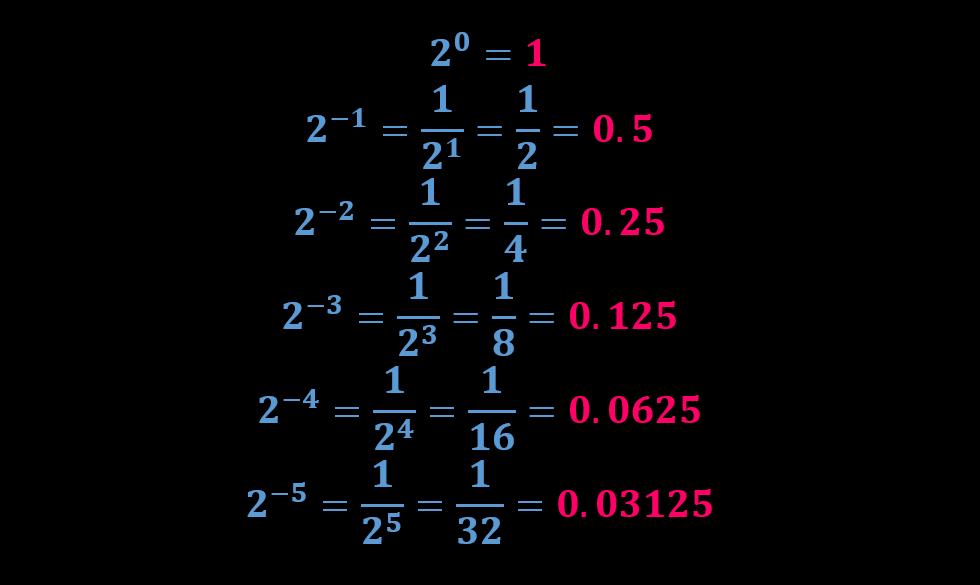
بنابراین معادل دسیمال، کسر باینری ۰.۱۰۱۱ با توجه به وزن هر یک از ارقام به صورت زیر معرفی خواهد شد.

در این مثال، کسر باینری ۰.۱۰۱۱ معادل عدد کسری ۰.۶۸۷۵ دسیمال خواهد بود.

مثال ۱

معادل دسیمال عدد کسری باینری ۱۱۰۱.۰۱۱۱ به صورت زیر محاسبه خواهد شد.

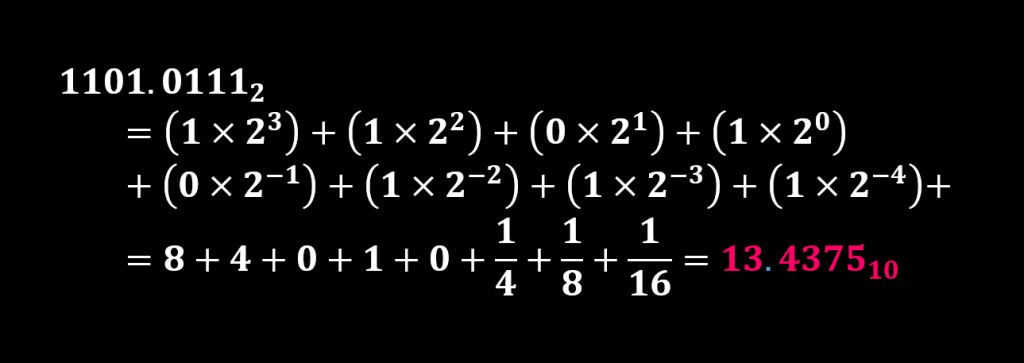
بنابراین مجموعه اعداد باینری کسری شامل ارقام باینری با وزن کمتر از ۱ (۰^۲) خواهد بود، که مشابه با قوانین حاکم در ریاضیات، هر عدد با توان منفی می‌­تواند به صورت کسری با مخرج توان مثبت معرفی شود.

تبدیل اعداد دسیمال به کسر باینری (Converting Decimal to a Binary Fraction)

در تبدیل اعداد کسری دسیمال به اعداد باینری کسری از روش مشابه با اعداد صحیح استفاده خواهد شد. با این تفاوت که، به جای تقسیم‌­های متوالی بر ۲ جهت مشخص کردن قسمت کسری از روش ضرب‌­های متوالی در ۲  استفاده خواهد شد.

بنابراین جهت تبدیل عدد دسیمال کسری به عدد باینری کسری قسمت صحیح عدد به صورت جداگانه و با استفاده از روش تقسیم‌­های متوالی بر ۲ و قسمت کسری (از سمت چپ به راست) با استفاده از روش ضرب­‌های متوالی بر ۲ محاسبه خواهند شد.

روش تقسیم­‌های متوالی بر دو یکی از متداول‌ترین روش­‌ها جهت تبدیل قسمت صحیح عدد دسیمال به اعداد باینری است. در این روش عدد دسیمال به صورت متوالی بر دو تقسیم خواهد شد تا زمانی که خارج قسمت برابر صفر شود. از کنار هم قرار دادن تمام باقی مانده­‌ها به ترتیب از آخرین باقی مانده (MSB) به اول (LSB) معادل باینری عدد دسیمال بدست خواهد آمد.

بنابراین معادل باینری عدد صحیح دسیمال ۱۱۸ به صورت زیر محاسبه خواهد شد.

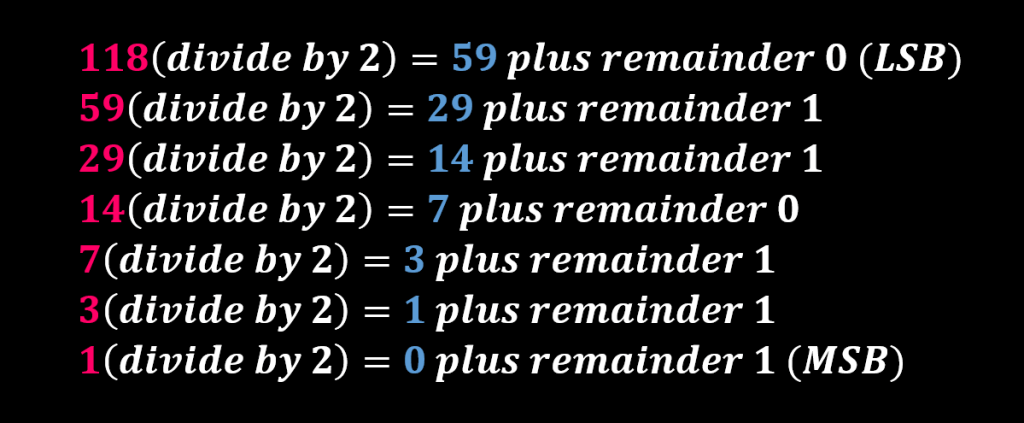
معادل باینری عدد صحیح ۱۱۸ برابر با عدد ۱۱۱۰۱۱۰ است.

معادل باینری بخش کسری عدد دسیمال با استفاده از روش ضرب متوالی بر 2 محاسبه خواهد شد. در این روش عدد دسیمال به صورت متوالی بر دو ضرب خواهد شد تا زمانی که بیت (carry) (بیت موجود در سمت چپ نقطه باینری) برابر صفر شود.

به این ترتیب، زمانی که حاصل فرآیند ضرب بزرگتر از عدد یک باشد، (carry) برابر با یک و اگر حاصل فرآیند ضرب کمتر از یک باشد، (carry) برابر با صفر خواهد بود.

در صورتی که فرآیند ضرب متوالی به سمت صفر میل نکند، عدد کسری دارای طول بینهایت خواهد بود و  با توجه به دقت مورد نیاز، تعداد معادل بیت­ها­ی بدست آمده به عنوان مثال ۸ و یا ۱۶ بیت در نظر گرفته خواهد شد.

بنابراین معادل کسر باینری عدد کسری دسیمال ۰.۸۱۲۵ به صورت زیر محاسبه خواهد شد.

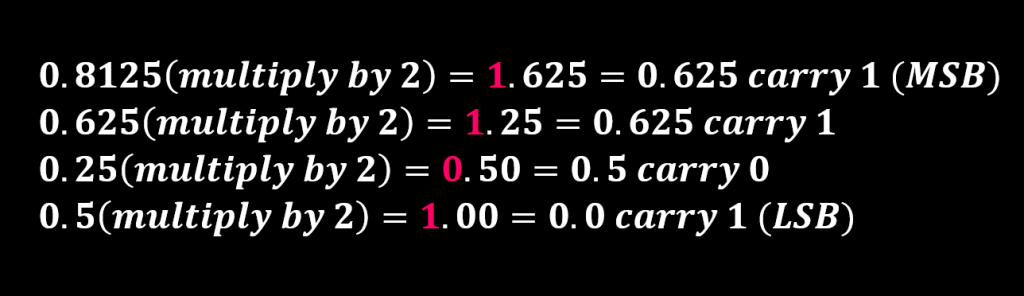
معادل باینری عدد کسری ۰.۸۱۲۵ برابر با عدد ۰.۱۱۰۱ است.

همچنین می­‌توان پاسخ فوق را با استفاده از روش بالا جهت تبدیل کسر باینری به معادل کسری دسیمال به صورت مجدد بررسی کرد:

مثال ۲

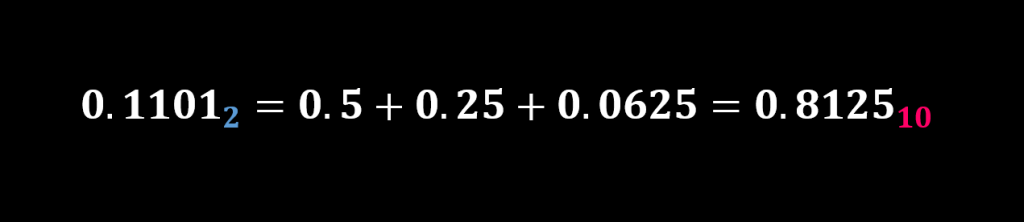
معادل کسر باینری عدد کسری دسیمال ۵۴.۶۸۷۵ به صورت زیر محاسبه خواهد شد.

در گام نخست با استفاده از روش تقسیم‌­های ۲، عدد صحیح ۵۴ به عدد باینری تبدیل خواهد شد.

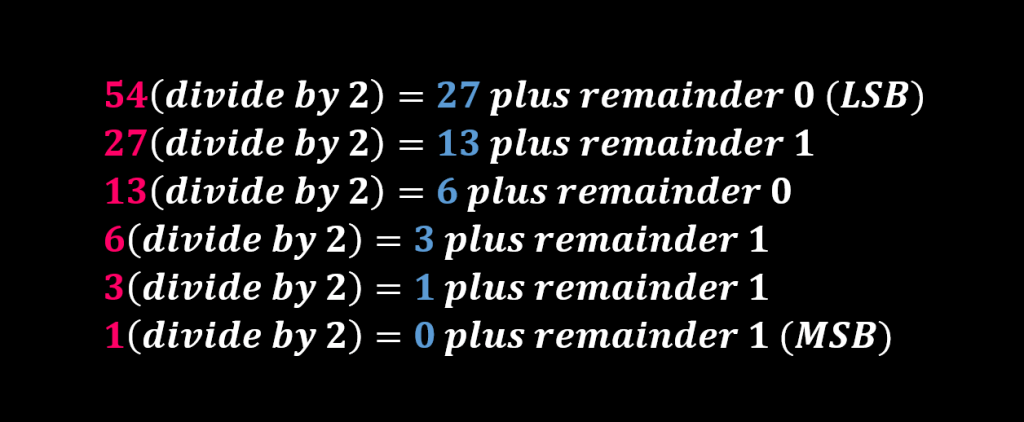
بنابراین معادل باینری عدد صحیح ۵۴ برابر با عدد ۱۱۰۱۱۰ است.

سپس عدد دسیمال کسری ۰.۶۸۷۵ با استفاده از روش ضرب متوالی در ۲ به کسر باینری تبدیل خواهد شد.

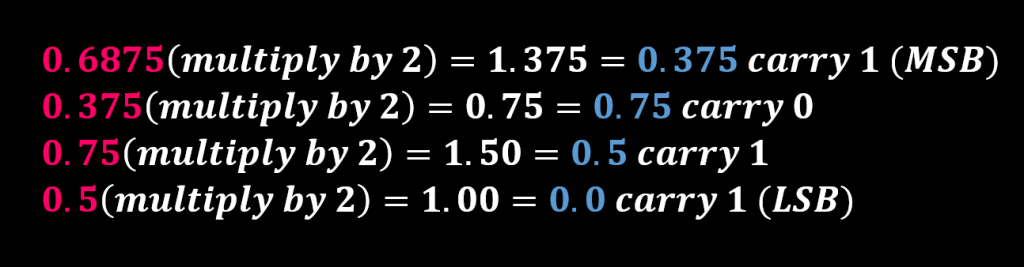
معادل باینری عدد کسری ۰.۶۸۷۵ برابر با عدد ۰.۱۰۱۱ است.

در نهایت با کنار هم قرار دادن دو بخش صحیح و کسری، معادل باینری عدد دسیمال ۵۴.۶۸۷۵ با عدد باینری ۰.۱۰۱۱ برابر خواهد بود.

خلاصه

جهت تبدیل هر عدد کسری دسیمال به معادل کسری باینری آن، کافیست پس از محاسبه حاصل ضرب عدد دسیمال در عدد 2، رقم (carry) (رقم موجود در سمت چپ نقطه باینری (ممیز)) یادداشت شود. مقدار رقم (carry) همواره برابر با 0 و یا 1 خواهد بود.

سپس عمل ضرب مجددا برای بخش کسری عدد حاصل از مرحله پیشین تکرار خواهد شد، و این عملیات تا حصول رقم (carry) برابر صفر ادامه خواهد داشت.

اعداد باینری کسری به صورت عدد ۲ با توان منفی نمایش داده خواهد شد.

جهت تبدیل اعداد دسیمال دارای بخش کسری و صحیح از دو روش تقسیم‌­های متوالی و روش ضرب متوالی استفاده خواهد شد. به این ترتیب، جهت تبدیل بخش صحیح دسیمال به عدد باینری از روش تقسیم متوالی و جهت تبدیل بخش کسری از روش ضرب متوالی استفاده می­‌شود.

همچنین بخش صحیح یک عدد دسیمال همواره دارای یک معادل باینری دقیق است، اما قسمت کسری دسیمال ممکن است دارای پاسخ صریح نباشد، زیرا بخش کسری دسیمال، می‌تواند کسری تکراری را ایجاد کند که منجر به تولید بی نهایت عدد باینری می‌شود.